01背包问题

最近两周是程序设计实验周，现在过去了一周，这一周可谓是非常的烧脑，学习了很多算法的设计，这篇博客就作为，算法笔记的开篇

对于开发程序来说程序 = 算法 + 数据结构算法对于程序员极其重要，这篇博客就依次记录一个经典的动态规划问题：

0/1背包
给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

分析一下题目，每一件物体都有装和不装两个选项（这也是0/1的来源），如果暴力穷举的话，每一次都要去比较价值，就非常麻烦

于是这题采用的算法思路是一个很经典的动态规划（dynamic programing）的思想

int weight[];
int value[];

先确定dp数组和下标的含义

dp[i][j]表示从下标0-i的物品取任意物品放进容积为j的背包的价值总和

然后是推导dp[i][j]数组，已知每一个物体都有两种状态

• 如果不放这个物体，那就代表dp[i][j] = dp[i-1][j],i-1就代表不放这第i的物体

• 如果放了这个物体呢，那么此时的背包价值dp[i][j]就可以用dp[i-1][j-weight[i]]+value[i]表示，这个含义就是放i这个物体的价值+背包容量变为j-weight[i]时的价值

所以如果要找到最大价值可以调用C++中的#include<algorithm>中的max函数

所以即为

dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])

下一步是初始化数组

如果j为0，也就是背包容积为0，价值也一定为零，所以dp[i][0]=0，如果i为0，也就是放下标为0物体，价值也就是value[0]的价值，自己设置即可（当然也可以不这也初始化，全部初始化为零也行，因为最后比的是最大值）

所以具体代码实现过程为

for(int i = 1; i <= num; i++){
        for(int j = 1; j <= MaxWeight; j++){
            if(j >= w[i]){
                dp[i][j] = max(dp[i-1][j],dp[i-1][j - weight[i]]+value[i]);
            }else{
                dp[i][j] = dp[i-1][j];
            }
        }
    }

这样看过来感觉很容易，但实际上问题就在于，到底代码的实现逻辑是什么？

就可以通过将dp[i][j]数组打印出来看看到底怎么回事

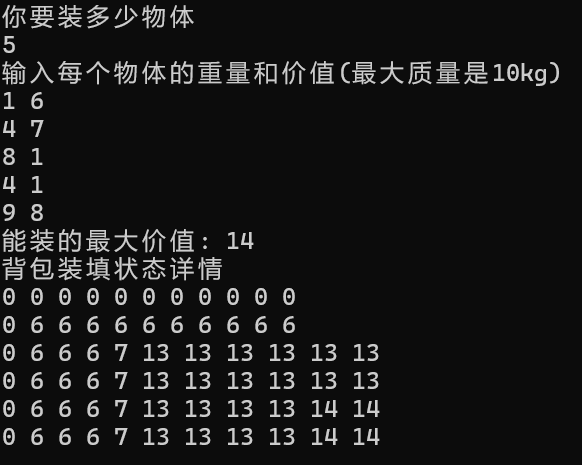
可以发现我是采用初始化全为0的方式，从第二行开始看，此时判断了放入重量为1的物体，总价值就是6，看看何时会改变，在第三行表示选择放入2的价值变化，从6 先变成了 7再变成了13，什么意思呢，当我发现我能放下 重量为 4的物体且此时背包价值刚好为7，背包如果再大的话就会加上物体1的价值，也就是13，剩下的思路也是如此分析

可以发现动态规划一个关键点是找到规划数组的方程，在这个二维方程的每一个位置都是储存了价值最大的状态，当往后选择时，就会调用前面的状态作比较，于是最终得到背包里的最大值

附上我的源代码

#include<iostream>
#include<algorithm>
using namespace std;
const int MAX = 100;
int  main(){
    const int MaxWeight = 10;
    int num;
    cout << "你要装多少物体\n";
    cin >> num;
    int v[num], w[num];
    cout << "输入每个物体的重量和价值(最大质量是10kg)\n";
    for(int i = 1; i <= num; i++){
        cin >> w[i] >> v[i];
    }
    int dp[MAX][MAX] = {0};
    for(int i = 1; i <= num; i++){
        for(int j = 1; j <= MaxWeight; j++){
            if(j >= w[i]){
                dp[i][j] = max(dp[i-1][j],dp[i-1][j - w[i]]+v[i]);
            }else{
                dp[i][j] = dp[i-1][j];
            }
        }
    }
    cout << "能装的最大价值: " << dp[num][MaxWeight] << endl;
    cout << "背包装填状态详情\n";
    for(int i = 0;i <= num; i++ ){
        for(int j = 0;j <= MaxWeight;j++){
            cout << dp[i][j] << " ";
        }
    //1 6 4 7 8 1 4 1 9 8测试集
        cout << endl;
    }
}